Selasa, 17 Desember 2019

Pengujian Hipotesis


Pengertian Uji Hipotesis dan Jenis-jenisnya 
 Uji Hipotesis adalah cabang Ilmu Statistika Inferensial yang dipergunakan untuk menguji kebenaran suatu pernyataan secara statistik dan menarik kesimpulan apakah menerima atau menolak pernyataan tersebut. Pernyataan ataupun asumsi sementara  yang dibuat untuk diuji kebenarannya tersebut dinamakan dengan Hipotesis (Hypothesis) atau Hipotesa. Tujuan dari Uji Hipotesis adalah untuk menetapkan suatu dasar sehingga dapat mengumpulkan bukti yang berupa data-data dalam menentukan keputusan apakah menolak atau menerima kebenaran dari pernyataan atau asumsi yang telah dibuat. Uji Hipotesis juga dapat memberikan kepercayaan diri dalam pengambilan  keputusan  yang bersifat Objektif.
Contoh dari Pernyataan Hipotesis yang harus diuji kebenarannya antara lain :
mesin solder satu lebih baik daripada dua
Metode baru dapat menghasilkan Output yang lebih tinggi
Bahan Kimia yang baru aman dan dapat digunakan
Pengambilan Keputusan dalam uji Hipotesis dihadapi dengan dua kemungkinan kesalahan yaitu :
Kesalahan Tipe I (Type I Error)
Kesalahan yang diperbuat apabila menolak Hipotesis yang pada hakikatnya adalah benar. Probabilitas Kesalahan Tipe I ini biasanya disebut dengan Alpha Risk (Resiko Alpha). Alpha Risk dilambangkan dengan simbol α.
Kesalahan Tipe II (Type II Error)
Kesalahan yang diperbuat apabila menerima Hipotesis yang pada hakikatnya adalah Salah. Probabilitas KesalahanTipe II ini biasanya disebut dengan Beta Risk (Resiko Beta). Beta Risk dilambangkan dengan simbol β
Dalam Pengujian Hipotesis, diperlukan membuat 2 pernyataan Hipotesis yaitu :
Pernyataan Hipotesis Nol (H0)
  • Pernyataan yang diasumsikan benar kecuali ada bukti yang kuat untuk membantahnya.
  • Selalu mengandung pernyataan “sama dengan”, “Tidak ada pengaruh”, “Tidak perbedaan”
  • Dilambangkan dengan H0
  • Contoh : H0 : μ1 = μ2 atau H0 : μ1 ≥ μ2
Pernyataan Hipotesis Alternatif (H1)
  • Pernyataan yang dinyatakan benar jika Hipotesis Nol (H0) berhasil ditolak.
  • Dilambangkan dengan H1 atau HA
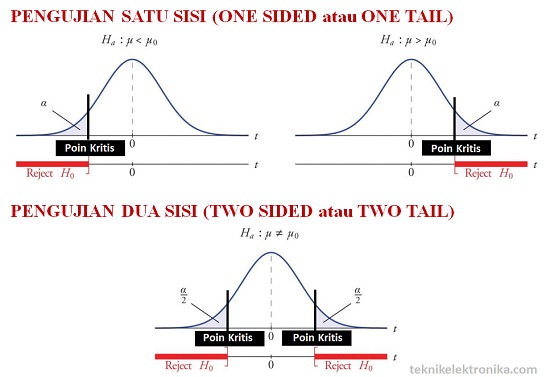
  • Contoh H1 : μ1 ≠  μ2 atau H1 : μ1 > μ2Dalam menentukan Formulasi Pernyataan H0 dan H1, kita perlu mengetahui Jenis Pengujian berdasarkan sisinya. Terdapat 2 Jenis Pengujian Formulasi Ho dan H1, antara lain :
    Pengujian 1 (Satu) Sisi (one tail test)
    Sisi Kiri
    H0 : μ = μ1
    H1 : μ < μ1
    Tolak H0 bila t hitung < -t tabel
    Sisi Kanan
    H0 : μ = μ1
    H1 : μ > μ1
    Tolak H0 bila t hitung > t tabel
    Pengujian 2 (Dua) Sisi (two tail test)
    H0 : μ = μ1
    H1 : μ ≠ μ1
    Tolak H0 bila t hitung > t tabelTolak H0 bila t hitung > t tabel
    Jenis-jenis Uji Hipotesis

Jenis-Jenis Statistik Uji Hipotesis yang sering digunakan

1 sample z test (Pengujian z satu sample)

1 sample z test digunakan jika data sample melebihi 30 (n > 30) dan Simpangan Baku (Standar Deviasi) diketahui.
Silakan lihat Tabel untuk Rumus 1 sample z test

1 sample t test (Pengujian t satu sampel)

1 sample t test digunakan apabila data sample kurang dari 30 (n < 30) dan Simpangan Baku tidak diketahui.
Silakan lihat Tabel untuk Rumus 1 sample t test.

2 sample t test (Pengujian t dua sampel)

2 sample t test digunakan apabila ingin membandingkan 2 sampel data.
Silakan lihat Tabel untuk Rumus 2 sampel t test.

Pair t test (Pengujian pasangan t)

Pair t test digunakan apabila ingin membanding 2 pasang data.
Silakan lihat Tabel untuk Rumus Pair t test

1 Proportion test (PengujianProporsi 1 (satu) sampel)

1 Propostion test digunakan untuk menguji Proporsi pada 1 populasi
Silakan lihat Tabel  untuk Rumus 1 Proportion test

2 Proportion test (PengujianProporsi 2 (dua) sampel)

2 Proportion test digunakan untuk menguji Perbanding Proporsi 2 populasi
Silakan lihat Tabel  untuk Rumus 1 Proportion test
Rumus Uji Hipotesis
Keterangan :
t = t statistik
z = z statistik
df = derajat kebebasan (degree of freedom)
= Rata-rata (Mean) sample
μ = Rata-rata Populasi
n = Jumlah sample
σ = Simpangan Baku Populasi
s = Simpangan Baku Sample
d0 = Dugaan rata-rata populasi
= Proporsi Sample
Langkah-langkah dalam membuat Uji Hipotesis
  1. Tentukan Formulasi Hipotesis Nol dan Hipotesis Alternatif
  2. Tentukan Taraf Nyata (α) atau disebut juga Level of Significant
  3. Tentukan Nilai Kritis (nilai Tabel) dan Statistik Uji Hipotesis-nya.
  4. Hitung Nilai Statistik Uji Hipotesis
  5. Pengambilan keputusan

Contoh Kasus  (Uji Hipotesis 2 sample t test) :
Seorang Engineer ingin melakukan pengujian Hipotesis terhadap Mesin yang ditawarkan oleh Vendor Mesin. Engineer tersebut kemudian mengumpulkan data sebagai berikut :
Mesin baru berhasil memproduksi rata-rata 550 unit perjam dalam waktu percobaan adalah 8 Jam produksi dengan simpangan bakunya  adalah 25 unit, sedangkanMesin lama berhasil memproduksi rata-rata  500 unit dalam waktu percobaannya adalah 8 Jam dengan simpangan bakunya adalah 20 unit. Apakah Mesin baru lebih baik dari Mesin Lama?

Penyelesaian :
Langkah1 : Formulasi H0 dan H1
H0 = μ1 = μ2
H1 : μ1 > μ2
Langkah2 : Tentukan Taraf Nyata (α) / Level of Significant
α  = 0.05 atau 5%
Langkah3 : Tentukan Nilai Kritis (Lihat Tabel t)
df = n1 + n2 -2
df = 8 + 8 -2
df = 14
ttabel  = 2.145
Karena Uji Hipotesis ini adalah membandingkan 2 sampel, maka Uji Hipotesis yang digunakan adalah 2 sample t test.
Langkah4 : Hitung Nilai Statistik Uji Hipotesis
Diketahui :
Mesin Barun1   = 8
X1  = 550
s 1   = 25
Mesin Laman2   = 8
X2  = 500
s 2   = 20
Rumus Uji Hipotesis 2 sample t test (silakan lihat tabel diatas)
Sp2 = ((8 – 1) (25)2 + (8 -1)(20)2 ) / (8 + 8 -2)
Sp2 = (4375 + 2800) /(14)
Sp2 = 512.5
Sp=  √512.5
Sp = 22.63
t =    (550 – 500 – 0)  / (22.63  √(1/8) + (1/8))
t = 4.418
Langkah 5 : Pengambilan Keputusan
4.438     > 2.145
thitung   >ttabel ,   → Tolak H0
Kesimpulan :
Berdasarkan Pengujian Hipotesis, Mesin Baru Lebih baik daripada Mesin Lama.

Diposting oleh di Tidak ada komentar:

Grafik

Grafik Batang Sederhana pada SPSS 




Satu gambar sering lebih bermakna dari seribu kata. Ungkapan ini sering dikemukakan untuk menunjukkan peran grafik dalam mendeskripsikan data, selain dengan menggunakan tabel distribusi frekuensi yang telah kita bahas pada tulisan-tulisan sebelumnya.
Untuk kepentingan itu, dalam beberapa seri tulisan dalam blog ini, akan kita bahas cara membentuk grafik dengan SPSS.
Sebagai latihan misalnya kita punya data tingkat pendidikan dan pendapatan dari 30 orang responden penelitian. Tingkat pendidikan misalnya dikategorikan sebagai:
1 = responden yang berpendidikan SLTP kebawah
2 = responden yang berpendidikan SLTA
3 = responden yang berpendidikan D3
4 = responden yang berpendidikkan S1.
Pendapatan juga kita kelompokkan atas tiga yaitu:
1 = pendapatan rendah (kurang dari Rp. 1.000.000)
2 = pendapatan menengah ( Rp. 1.000.000 – 3.000.000)
3 = pendapatan tinggi ( diatas Rp 3.000.000)
( Catatan: jika data yang dimiliki masih berupa data mentah (belum dikelompokkan), kita dapat mengelompokkannya dengan SPSS. Baca tulisan ini).
Data tingkat pendidikan dan pendapatan responden tersebut diberikan di bawah ini.

Setelah menginput data tersebut (atau bisa juga sebelum menginput data ), berilah value label untuk masing-masing kategori variabel yaitu untuk pendidikan: 1 (=< SLTP), 2(SLTA), 3(D3), 4 (S1) sedangkan untuk pendapatan: 1 (rendah), 2(menengah), 3(tinggi). Cara memberikan value label, silakan baca tulisan ini.
Terdapat tiga jalur (cara) dalam pembuatan grafik pada SPSS. Pada tulisan ini kita akan membahas cara yang paling sederhana saja, sebagai berikut:
Kklik Graphs > Legacy Dialogs. Akan terdapat beberapa pilihan grafik yang tersedia yaitu:
Bar (grafik batang)
3-D (grafik batang tiga dimensi)
Line (grafik garis)
Pie (grafik lingkaran)
High-Low
Boxplot
Error Bar
Population Pyramid
Scatter/Dot (sebaran/titik)
Histogram
Masing-masing grafik memiliki karakteristik-karakteristik tertentu yang sesuai dalam penggambaran data. Grafik yang berbasis batang, umumnya digunakan untuk menggambarkan perbandingan antar variabel/kategori. Grafik yang berbasis garis, umumnya (lebih sesuai) untuk menggambarkan perkembangan data. Grafik yang berbasis lingkaran, umumnya untuk menggambarkan data yang bersifat proporsi. Grafik yang berbasis titik umumnya untuk menggambarkan pencaran/sebaran data.
Dalam konteks data latihan kita, pada tulisan ini kita akan membahas terlebih dahulu mengenai grafik batang. Untuk itu klik Bar, akan muncul tampilan berikut:

Terdapat tiga pilihan grafik batang, yaitu Simple, Clustered dan Stacked. Pilihan Simple digunakan untuk menggambarkan grafik dari variabel tunggal. Pilihan Clustered dan Stacked digunakan untuk menggambarkan grafik dari variabel tunggal tetapi dikelompokkan berdasarkan kategori dari variabel lainnya. Pengelompokan pada tipe grafik Clustered dilakukan secara horizontal, sedangkan pada tipe Stacked secara vertikal.
Kemudian terdapat pilihan tampilan data untuk grafik (Data in Chart Are), yaitu diringkas berdasarkan kategori (Summaries for groups of cases), diringkas berdasarkan pemisahan variabel (Summaries of separate variables) atau menampilkan data individual. (Catatan: anda bisa mencoba-coba pilihan tersebut untuk memahami maknanya).
Sebagai latihan awal, kita akan membuat grafik untuk variabel jenis kelamin. Kita pilih jenis grafik Simple (klik) dan tampilan data adalah Summaries for groups of cases. Kemudian klik Define, akan muncul tampilan berikut:

Tentukan terlebih dahulu ukuran yang akan ditampilkan oleh batang dari grafik kita (Bar Represent). Ada beberapa pilihan yaitu ukuran frekuensi absolut (N of cases), kumulatif frekuensi (Cum.N), persentase frekuensi (% of cases), kumulatif persentase frekuensi (Cum.%), atau ukuran statistik lainnya (Other Statistics). Anda juga bisa mencoba-coba berbagai pilihan ini untuk melihat perbedaan output grafiknya.
Untuk latihan ini, kita pilih % of cases. Selanjutnya masukkan variabel Pendidikan ke dalam kotak Category Axis, dan kemudian klik OK. Akan muncul output grafik sebagai berikut:

Ok, sekian dulu, kita lanjutkan pada tulisan saya berikutnya,oh iya saya juga menambahkan video agar caranya dapat dilihat atau di praktekan lebih mudah;


                                                            

Diposting oleh di Tidak ada komentar:

Tabel Silang (Crosstab)


Analisis Tabulasi Silang (Crosstab)

Analisis tabulasi silang merupakan salah satu analisis korelasional yang digunakan utnuk melihat hubungan antar variable. Sehingga analisa tabulasi silang ini dapat digunakan untuk menganalisa lebih dari dua variable.
Berikut ini kami sajikan salah satu contoh perhitungan yang menggunakan analisis tabulasi silang atau crosstab.
Penelitian untuk mengetahui ada tidaknya hubungan antara jenis kelamin dengan prestasi kerja.
Ha   : terdapat hubungan jenis kelamin dengan prestasi kerja
Ho : tidak ada hubungan jenis kelamin dengan prestasi kerja.
Untuk membuktikan hipotesis tersebut hal yang terlebih dahulu dilakukan adalah membuat penelitian seperti mengadakan survei di suatu perusahaan atau organisasi. Data tersebut dapat diperoleh dari kuesioner yang dibagikan kepada beberapa responden. Dalam contoh ini, kita mengambil responden sebanyak 30 orang. Dari data tersebut dapat menghasilkan data seperti contoh berikut ini:
Untuk memudahkan analisa maka kita dapat membuat kode pada jenis kelamin dan prestasi kerja.
No
Jenis Kelamin
Prestasi Kerja
1.Value 1 = Laki-LakiValue 1 = Rendah misal skor 0-40
2.Value 2 = WanitaValue 2 = Sedang misal skor 41-80
3.Value 3 = Tinggi misal skor 81-120

Setelah data yang diperoleh diubah menjadi data nominal, yakni dengan memberi kode pada setiap variable maka dapat disajikan menjadi seperti tabel di bawah ini:
No
Jenis Kelamin
Prestasi Kerja
1
1
1
2
1
2
3
2
3
4
2
1
5
1
3
6
2
2
7
1
2
8
1
1
9
1
3
10
2
2
11
2
3
12
2
1
13
1
1
14
1
1
15
2
2
16
1
1
17
1
2
18
2
3
19
2
1
20
1
3
21
2
2
22
1
2
23
1
1
24
1
3
25
2
2
26
2
3
27
2
1
28
1
1
29
1
1
30
1
1
Setelah kita memberi kode seperti contoh tersebut di atas, maka kita telah siap untuk mengadakan analisa crosstab atau analisa tabulasi silang. Langkah-langkahnya sebagai berikut:
  1. Membuka program SPSS dengan cara
    • Double klik pada shortcut yang terdapat pada dekstop komputer
    • Atau dengan cara Start > All Program > SPSS for Windows
Kedua cara tersebut akan muncul tampilan SPSS yang mirip dengan tampilan Microsoft Excel.
2. Memasukkan data tabel tersebut dalam program SPSS
a. Masukkan variabel jenis kelamin dan variable prestasi kerja pada sheet Variabel View
Perlu diingat bahwa dalam kolom Name tidak boleh terdapat karakter spasi, sehingga untuk mengganti spasi tersebut dapat menggunakan karakter .
b. Dikarenakan variabel jenis kelamin dan prestasi kerja telah diubah menjadi data nominal yakni menggunakan kode seperti pada Tabel 2, maka dalam kolom Value perlu ditambahkan keterangan kode-kode tersebut dengan  cara:
  • Klik ikon di samping kanan tulisan None pada Kolom Value ,
  • Isikan kode “1†pada kotak Value, dan “Laki-Laki†pada kotak label. Klik Add.
  • Lakukan hal yang sama, masukkan kode “2†pada kotak Value, dan “Wanita†pada
  • Klik OK
  • Lakukan hal yang sama untuk variabel Prestasi Kerja.
  • Selanjutnya Klik Analyze > Descriptive Statistic > Crosstab.
  • Masukkan variable “Jenis Kelamin [jenis_kelamin]†pada kotak Row(s) dengan cara klik tanda panah yang terdapat pada samping kiri kotak Row(s) tersebut.
  • Masukkan variabel “Prestasi Kerja [prestasi_kerja]†pada kotak Column(s) dengan cara klik tanda panah yang terdapat pada samping kiri kotak Column(s) tersebut.
  • mudian Klik “Statistics..†sehingga akan muncul jendela baru. Beri tanda centang (v) pada kotak Chi Square. Klik Continue.
    1. Klik “Cells..â€, sehingga akan muncul jendela baru. Beri tanda centang (v) pada kotal  “Observedâ€, “Expectedâ€, “Rowâ€, “Columnâ€, “Totalâ€. Dan Klik Continue.
    1. Klik OK.
    2. Setelah itu, secara otomatis output akan keluar.
    Case Processing Summary
    Cases
    Valid
    Missing
    Total
    N
    Percent
    N
    Percent
    N
    Percent
    Jenis Kelamin * Prestasi Kerja
    30
    100.0%
    0
    .0%
    30
    100.0%

    Penjelasan output SPSS:

    Pada tabel “Case Processing Summaryâ€, menunjukkan dalam penelitian tersebut terdapat 30 sampel. Tidak ada yang hilang atau missing sehingga tingkat kevalidannya adalah 100%.
    Jenis Kelamin * Prestasi Kerja Crosstabulation
    Prestasi Kerja
    Total
    Rendah
    Sedang
    Tinggi
    Jenis KelaminLaki-LakiCount
    9
    4
    4
    17
    Expected Count
    7.4
    5.1
    4.5
    17.0
    % within Jenis Kelamin
    52.9%
    23.5%
    23.5%
    100.0%
    % within Prestasi Kerja
    69.2%
    44.4%
    50.0%
    56.7%
    % of Total
    30.0%
    13.3%
    13.3%
    56.7%
    WanitaCount
    4
    5
    4
    13
    Expected Count
    5.6
    3.9
    3.5
    13.0
    % within Jenis Kelamin
    30.8%
    38.5%
    30.8%
    100.0%
    % within Prestasi Kerja
    30.8%
    55.6%
    50.0%
    43.3%
    % of Total
    13.3%
    16.7%
    13.3%
    43.3%
    TotalCount
    13
    9
    8
    30
    Expected Count
    13.0
    9.0
    8.0
    30.0
    % within Jenis Kelamin
    43.3%
    30.0%
    26.7%
    100.0%
    % within Prestasi Kerja
    100.0%
    100.0%
    100.0%
    100.0%
    % of Total
    43.3%
    30.0%
    26.7%
    100.0%

kesimpulannya bahwa Pada tabel “Jenis Kelamin * Prestasi Kerja Crosstabulation†menunjukkan data objektif/ frekuensi nyata (Count) dan frekuensi harapan (Expected Count) baik dalam bentuk skor maupun presentase.
Berikut hasilnya:
Dari penelitian tersebut terdapat 9 karyawan laki-laki yang memiliki prestasi kerja rendah, 4 karyawan laki-laki berprestasi kerja sedang dan 4 sisanya berprestasi tinggi.
Sedangkan untuk karyawan wanita, 4 wanita mempunyai prestasi kerja rendah, 5 orang memiliki prestasi kerja sedang dan 4 orang lainnya mempunyai prestasi kerja tinggi.


Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)